All done here! Check out our other subjects!
Core
Case - an individual with a disease or condition of interest.
Control - an individual without a disease or condition of interest used as a comparison.
Exposure - a factor which is being studied to determine whether it affects disease development.
Epidemiology - The study of the distribution and determinants of health and disease in populations, and the application of this study to control health problems.
Random error - The chance that every study has that the results are influenced by chance rather than causal relationship. The effect of random chance is ubiquitous and can only be diluted by increasing sample sizes.
Systematic error - A consistent bias in the design, conduct, or analysis of a study that leads results away from the true value.
External validity - How similar/ representative a sample is to the whole population. Used for generalising results to the whole population, e.g. it can’t be assumed that because a group of all men acted a certain way, that a mixed gender population would act the same.
Internal validity - How similar the groups within the experiment are to each other, e.g. a control group of all men would not be comparable to an experimental group of all women.
Recall error - Errors in recollection that can occur if studies are done retrospectively.
Observer error - Errors in what the observer records because of their pre-conceived expectations. This is combated by blinding observers to which group is which.
Measurement error - Errors arising from inaccurate measurement, such as instrument calibration problems, observer variation, or faulty equipment.
Accuracy- How close the data measured is to the true value.
Precision - How close points in a data set are to each other.
Prevalence, incidence and risk
The below use fictitious figures regarding lightning strikes in the UK. Any figures on Asthma are derived from this source.
Prevalence - The proportion of people who have a disease at a given time in a population. Calculated by dividing number of cases by total population. E.g. 8 million people in the UK have a diagnosis of asthma.
Incidence - Number of new cases of a disease within a certain time frame, worked out by dividing number of new cases by population years at risk. E.g. 160,000 people a year develop asthma in the UK.
Incidence rate ratio - The ratio of the incidence rates of two groups, taking into account the person-time at risk in each group.
Odds - The chance of someone getting the outcome (disease) versus not getting the outcome. Calculated dividing cases by non-cases. For example if 1264 people walk on hills during thunderstorms 5 will get struck by lightning. 5/1264 = 0.004 in 1 chance of being hit by lightning. Or by multiplying by 250 (1/0.004 = 250) this same odds can be expressed as a 1 in 250 chance of being struck by lightning. So for every 250 people who walk on a hill in a thunderstorm one of those 250 will be struck by lightning.
Odds ratio - A method of comparing the odds of developing a condition (outcome of interest) between two groups (case and control). If the odds ratio is 1 there is no difference between the groups. For example if we compare lightning strikes suffered by those walking on a clear day (control) (1 individual out of 684 - 1 in 684 chance) versus the total number of strikes on those walking during a thunderstorm (2 individuals out of 832 - 1 in 416 chance) and compare the two groups 1 in 416: 1 in 684 - 416:684 - 1:1.6. As a the odds ratio is +1 (1.6) there is a positive relationship between lightning strikes and thunderstorms.
Absolute risk - The probability of developing a disease over a specified period of time in a defined population.
Relative risk - Ratio of absolute risk of two groups. For example ‘you are twice as likely to get hit by lightning in Scotland than in England’ (this is not true). This statement can be misleading however as the absolute risk may be very small e.g. 5 cases of lightning strikes in England vs 10 in Scotland. Although it is true to say you are twice as likely to get struck the absolute risk is in fact very low.
Risk difference - Difference between the absolute risk data for two groups. Using the above example the risk difference would be 5 (which is much less dangerous sounding than 2x more likely).
Confounder - A factor that affects the independent variable (exposure) and the dependent variable (disease) and distorts the relationship between them. These cannot always be known about or adjusted for (though it should be attempted).
Standardisation - A method of adjusting for confounding variables to minimise their effects.
Retrospective - When a study occurs now, looking at exposures in the past and current disease state.
Prospective - When a study begins now, looking at people who have just been exposed to something and their future development of the disease.
Population years - The years at risk of each member of the population all added together, e.g. if ten factory workers were exposed for five years each, the population years would be 50 years.
Inverse Care Law - Resources are more easily available to the more affluent in society. This reinforces the inequity present in the healthcare system already.
Inequality Paradox - The most needy fail to get what they need even if their needs are addressed
specifically, because the more affluent adapt easily to changes in their healthcare, e.g. they
might be able to take time off work more easily if they’re not on inflexible shift work.
Proportionate Universalism - Combating the problems raised by the inequality paradox. For example, universal child benefit is given out the same to everyone without means testing so more people can access it. This is useful because benefits that are means tested by their nature are more complex and inaccessible to those that require the benefits the most e.g. poorer literacy in a deprived population means paperwork can’t be properly filled in and benefits accessed.
First Order Problem Solving - Immediate solving of the problem with a quick fix that won’t solve the problem long term.
Second Order Problem Solving - Slower forms of problem solving that fix the root cause of the problem; takes longer initially, but the problem is fully fixed.
Moral Individualism - A self-centred approach to problems that doesn’t help the greater good. An example of this is to say that a person who smokes is self-centred, because they care more about the five minutes they get to themselves when they have a cigarette than the effects it would have on their family if they got lung cancer.
James Reason's Framework of Error
- Active Failures - Actions that lead directly to harm, e.g. slips or mistakes.
- Latent Failures - Any aspect of context that makes active failures more likely, e.g. poor supervision, lack of checks, poor training.
Screening Test Terms
Positive Predictive Value - The probability that someone who tested positive actually has the disease.
Negative Predictive Value - The probability that someone who tested negative is actually healthy.
Sensitivity - The proportion of people with the disease who test positive (proportion of true positives).
Specificity - The proportion of people without the disease who test negative (proportion of true negatives).
Case Control
Cases versus control, using past exposure.
E.g. Asthma versus not asthma, using past mouldy house as the past exposure.

Table - Cases vs Controls in exposed and unexposed circumstances
SimpleMed original by Dr. Maddie Swannack
Odds of an exposure having an effect = a/c
Odds of an exposure not having an effect = b/d
Odds ratio = a/c divided by b/d = ad/bc
Issues: selection bias, random error.
Cohort
Exposed versus unexposed now, investigate future cases - prospective.
Exposed versus unexposed past, follow up into the future - retrospective.
Person years at risk = years that each person in a population has been at risk all added together.
Incidence rate of exposed = development of outcome in exposed / person years at risk.
Incidence rate ratio = IR exposed / IR unexposed = how much more likely the disease is to occur with the exposure.
Issues: loss to follow up (survivor bias), observation bias, random error.
Cross Sectional
Find cases right now in the population - this is a snapshot.
An example is in 2001 there were 250,000 cases of asthma compared to in 2011 when there were 300,000 cases.
Prevalence / Absolute Risk = number of people with disease / total population.
Issues: sampling bias, participant bias, random error.
Ecological
Look at whole population, separate by a characteristic (usually geographical), look at cases in each group.
E.g. difference in cases of asthma at different distances from a road.
Issues: characteristics may be unclear, confounding variables, lack of generalisability (depending on sample size), random error.
Confidence Intervals
For case control and cohort studies:
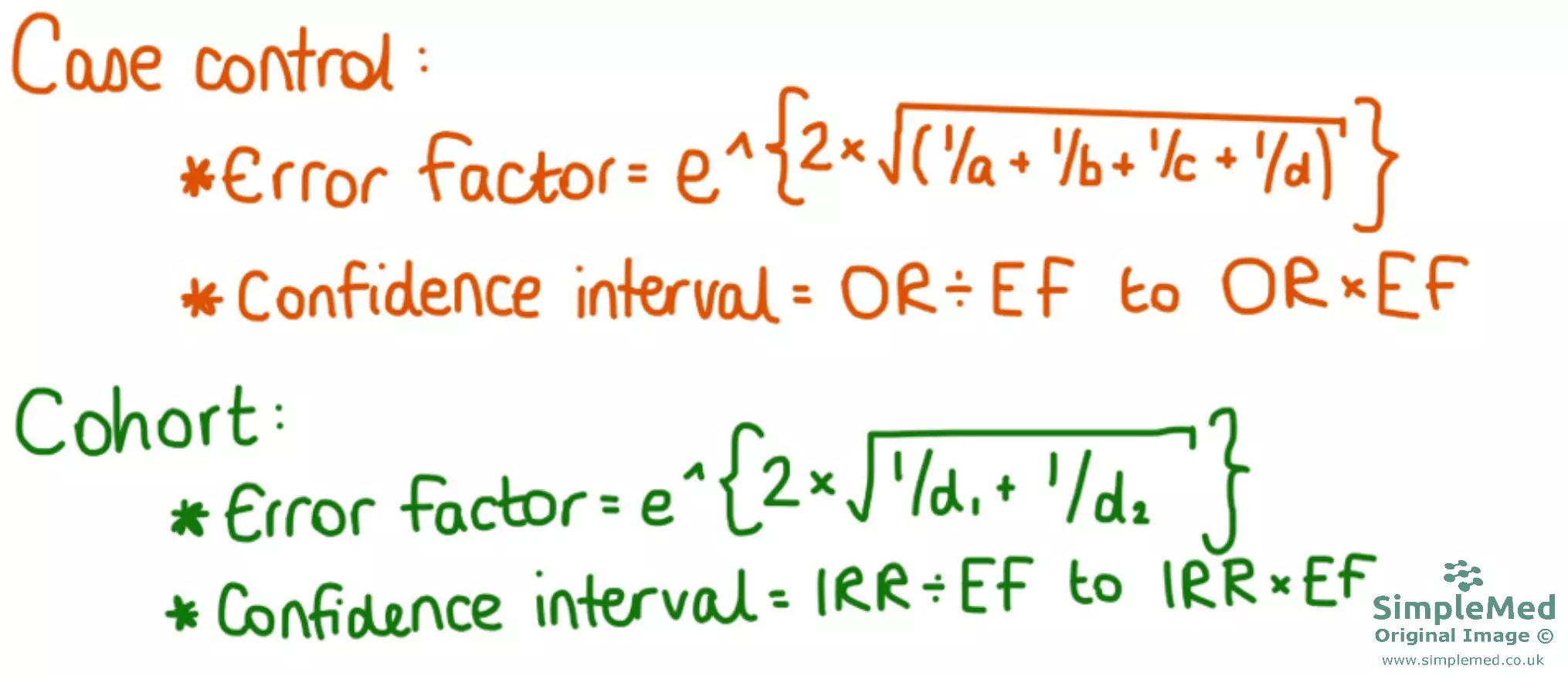
Figure - The equations used to work out the error factor and the confidence intervals of cohort and case control studies
SimpleMed original by Dr. Maddie Swannack
For cross sectional studies:
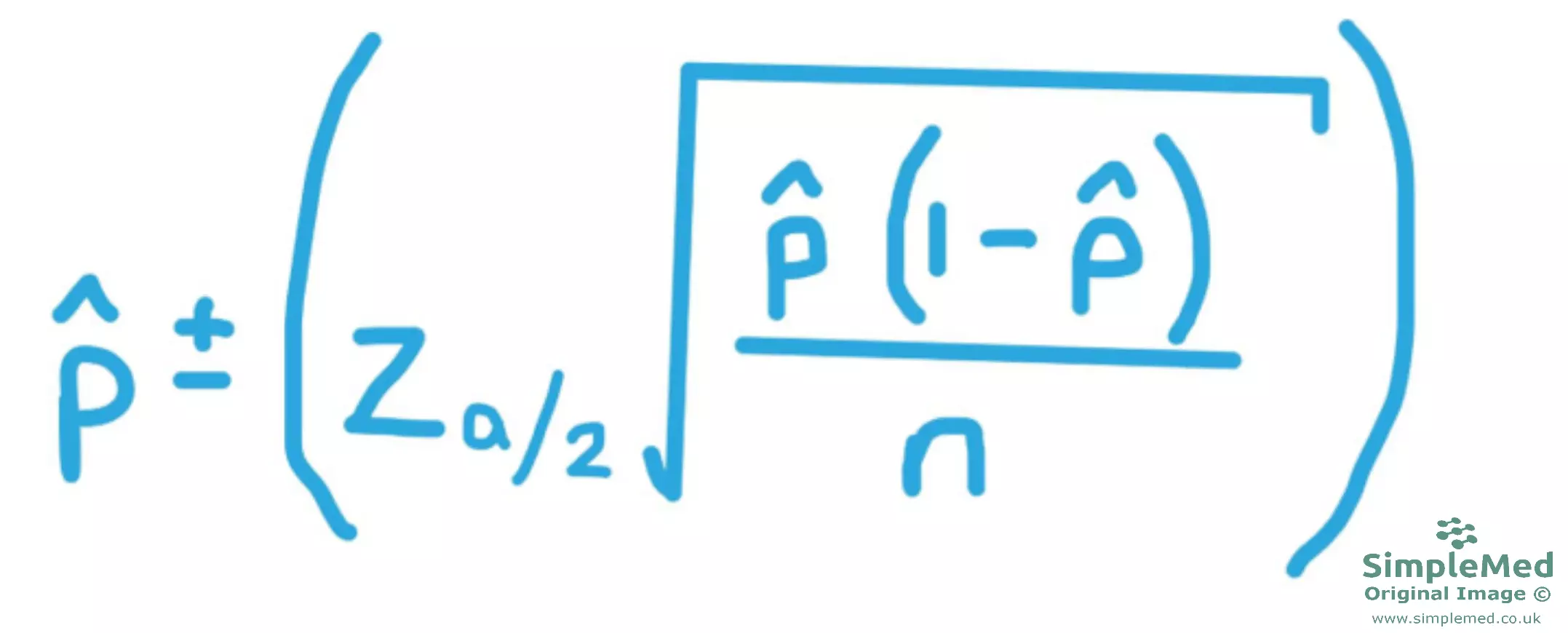
Figure - The equation used to find the confidence interval of a cross sectional study
SimpleMed original by Dr. Maddie Swannack
The null hypothesis is represented by either the number 1 (if using ratios) or the number 0 (if using the difference between results - less common). If this number lies within the confidence interval the results are not statistically significant. This is because the null hypothesis is that there is no relationship between the variable - if the difference between two numbers is 0 they are the same - if a ratio of two factors are 1 it is the same. If the confidence interval is large enough to include the null hypothesis, this means that the true value may be the null hypothesis (no difference) as the true value lies within the confidence interval 95% of the time (when using a 95% confidence interval). This means that the null hypothesis could be true and the study cannot prove an association between the variables i.e. the result is not statistically significant.
It is important to remember that it is the number representing the null hypothesis that needs to fall outside the confidence interval for the study to be considered statistically significant. The study data will always be in the confidence interval, as the confidence interval is a range based around this value.
It is the number representing the null hypothesis that is important.
Edited by: Dr. Ben Appleby
Reviewed by: Dr. Thomas Burnell
- 5261

