Get in Touch
Contact Us
Click here for our Contact Form
Next Lesson - Models of Health
Core
See our summary and glossary article which explains the terms used in this article.
There are four main types of observational studies used in the study of populations.
They are split into descriptive (where the outcome is a qualitative or wordy description of the findings) and analytical (where the outcome is a quantitative or numerical value representing the findings).
The two types of descriptive study discussed in this article are ecological and cross-sectional studies, and the two analytical studies discussed are cohort and case-control studies.
Throughout this article, disease is used as the focus in every study design, and asthma is used as every example. This is done to make the study designs easier to compare. However, these study designs could be used for a wide variety of epidemiological hypotheses, and their use is not limited to disease investigations.
A “Case” in this article refers to a study participant that has the disease. A “Control” is a study participant that does not have the disease/ has not been exposed to a factor but is included in the study for comparison.
Any numbers in this article are purely hypothetical and do not represent the true results of any known studies.
Common Flaws with Study Designs
All study designs have common flaws, relevant to all types. These are grouped together here so that they don’t have to be explained four times, as they apply to all four study designs.
Random error: It is important to remember that the most common error in all study design is random error, aka chance. It is impossible to completely remove this element, but many things can be done to help to reduce it and make its effect known, such as declaring confidence intervals in the results, increasing sample size or randomising which participants are in each of the study groups. Increasing sample size is a very useful tool to reduce random error as it dilutes the effects of chance.
Lack of general applicability/ generalisability: Lack of generalisability applies to any study where a sample of the population is chosen rather than studying the whole population. If the designer has taken 1000 people from the city of London to do their study, they cannot necessarily say that those 1000 people represent the 8.2 million other people in London. This means that their study would have low generalisability. This could be improved by increasing the sample size (number of people in the study) or sample pool (taking a group from each borough) but this is expensive.
Confounding variables: Confounding variables are external variables that influence individuals within the study that the study organisers may not necessarily know about. Confounders can affect both the dependent and independent variable. This means that the confounding variable could cause an inappropriate association between the independent and dependent variable (a false result). A relationship could be found between two variables which does not exist in isolation but is a direct result of the confounding variable. An example of this would be: the amount that a loaded bow is pulled back and how far the arrow flies. In theory, the more force that is applied, the further the arrow would fly one a direction. However, the confounding variable in this case would be the wind on that day - if the wind blows in different directions the flight of the arrow will be affected. Once identified this confounder can be controlled for e.g. trying the experiment on a windless day. Only then can a true association between distance drawn back and distance be established.
Ecological studies are the easiest study design to understand and an example of a descriptive study. They involve collecting a population of people, separating that group by a characteristic (usually geographical), and then looking at the occurrence of the disease (number of cases) in each group. As a result, they are fast to complete and cheap.
For example, the population of a town could be the target population for this study, and the characteristics that the population is being separated by could be distance from a motorway. If the disease investigated was asthma, the results of the study would be a set number, for example, “There are 4000 cases of asthma in residents less than a mile from the motorway compared to 3000 cases of asthma in residents more than a mile from the motorway.”
There are a number of flaws with the ecological study design:
- Confounding variables are common and difficult to expose.
- Lack of generalisability is common.
- Ecological fallacy – as data is gathered about the large groups or populations it can’t accurately be applied to individuals.
Cross sectional studies are a second type of descriptive study commonly used. To perform this study, the researcher must find the number of cases at a certain time within a group of the population. This ‘snapshot’ provides good information for prevalence but does not study exposure or any causal link. This study also is less helpful when studying rare diseases as it is likely that individuals will be missed in the sample size.
For example, “In 2015, there were 250,000 people with asthma in England.”
This study is commonly carried out via door-to-door surveying and other similar methods.
This study design also has multiple new terms associated with it:
- Absolute risk – this is also known as prevalence and is the number of people with the disease in the population divided by the total number of people in the population.
There are some flaws with the cross sectional study design:
- Sampling bias – this occurs when some members of the population are more likely to be selected to participate in the study. This could happen, for example, if the study takes place during the day. This would then exclude individuals who work during the day, and would therefore skew the results of the study because these people cannot be included. This would then mean that the study would not accurately represent the population.
- Participant bias – this is when the participant acts in a certain way because they think that is how the researchers wants them to behave. For example, if a patient knows whether they have been given the drug or the placebo in a drug trial, they might exaggerate or play down their symptoms. This can be unintentional on the part of the participant.
Because there is no comparison in a cross sectional study, it is not possible to form a null hypothesis. This means that an ‘alternative hypothesis’ is formed instead. This is an educated guess of the prevalence in a certain population. However, this is not particularly useful, so it is not often used.
Cohort studies are a common type of analytical study. They involve classifying the healthy participants based on their exposure and then investigating how many of each type go on to develop disease.
For example, if investigating the influence of mould in a home on the development of asthma, the participants would be classified into whether they had lived in a house with mould (the independent variable), and then the development of asthma would be the outcome of interest (the dependent variable). The study would then follow both classes or groups throughout their life to see if and when they develop asthma. This is useful as it can be used to demonstrate causal relationships between exposures (mould) and conditions (asthma).
Cohort studies can come in two types:
- Prospective cohort studies take participants who have just been exposed and investigate their future development of the disease.
- Retrospective cohort studies take participants who have been exposed in the past and investigate the development of the disease in the present. This is still classified as a cohort study because the participants are put in groups based on their exposure rather then based on their disease state.
Cohort studies also use some specific language terms;
Person years – the total number of years that all individuals in the study are observed for. A person is no longer observed when they die or when they leave the study. Person years is simply a measure of time. If 100 people are observed for 2 years, that is 200 person years.
Incidence rate - The incidence rate of the exposed population is worked out by dividing the number of people that developed the diseased in the exposed group by the 'person years at risk'. For example, if the exposed population (the people who had been living in the mouldy house) has spent an average of 5 years each at risk (living in the house)(calculated by total number of years at risk divided by number of individuals in the ‘exposed’ group), and 10 out of the 100 people develop asthma, the incidence rate would be 10 / 5, which is 2 cases per person year at risk – in the average time of 5 years 10 participants developed the condition therefore in 1 year 2 participants would develop the condition. The sample size in this group does not matter for working out the incidence rate, because this sample is included in the average person years at risk.
Incidence rate ratio – this is the ratio between the incidence rate of the exposed and the incidence rate of the unexposed. This shows how much more likely it is for a participant to have developed the disease if they have been exposed.
Cohort studies also have many issues:
- Loss to follow up – this is a flaw specific to prospective cohort studies as it follows individuals into the future. Inevitably some individuals will drop out of the study for various reasons leading to a loss of sample size. Two specific types of loss to follow up include:
- Survivor bias – Individuals who healthier are likely to stay on the study whereas those who develop other health conditions may be less able to maintain participation in the study and leave. This causes skewing the final sample and making it less representative of the general population.
- Differential loss – When individuals with specific characteristics leave the study this causes the remaining sample to become less representative of the general population. Observation bias – this error comes from a miscalculation error. If participants are asked to provide measurement or data there can be issues with incorrect reporting of results.
Cohort studies are usually expensive as they involve large sample sizes to mitigate loss to follow up and require the resources to follow up these large groups many years into the future. However cohort studies are very helpful for producing a large amount of data and allowing for prevalence and incidence to be calculated.
The following considerations should be made when designing a successful cohort study:
The acronym PICO can be used to remember what needs to be established when designing a cohort study.
Population – who will be sampled from?
Intervention – what is the exposure of interest
Comparison – who is being compared against, who is the control group from the sample population (those who lack exposure).
Outcome – what is the end condition being determined.
In our example
P – Children who live in x city.
I – the presence of mould in the family home.
C – children who live in the city in non mouldy houses.
O – development of asthma in 20 years.
Case control studies are the final type of study discussed in this article and are an analytical type of study. They involve finding participants who suffer from the disease (cases) and those who do not (controls) and looking into their past to see if they have been exposed. This means that case control studies are always retrospective.
For example, participants with asthma and participants without asthma are included, and everyone is investigated to see if they have been exposed to mould in their houses previously.
This data can be put into a simple table, as seen below.
Table - Cases vs Controls in exposed and unexposed circumstances for a case control study
SimpleMed Original by Maddie Swannack
This table can then be used to work out the following:
- The odds of exposure having an effect – exposed cases divided by unexposed cases or a/c.
- The odds of exposure not having an effect – exposed controls divided by unexposed controls or b/d
- This means that the odds ratio is worked out by doing a/c divided by b/d which simplifies to ad/bc. This means that the ‘expected results’ (exposed cases x unexposed controls) are divided by the ‘unexpected results’ (unexposed cases x exposed controls).
The issues with case control studies are the following:
- Selection bias – this is the bias that occurs naturally in this study design because there can be no element of randomisation with the groups that the participants are put in.
- Random error.
Case control studies are helpful as they are cost effective and do not require any follow up. They are also more useful in studying chronic diseases compared to cohort studies as they allow selection of already ill individuals.
However – these studies are susceptible to the effects of confounding variables and don’t allow for establishment of a temporal (time based) relationship to be found due to their retrospective nature. Furthermore they can’t be used to calculate prevalence or incidence as only establishes if individuals have been exposed not when.
Confidence Intervals – Case Control and Cohort Study Designs
Numerical data produced from studies can only be trusted a certain amount due to the flaws mentioned above with each study design. Confidence intervals are the range of values in which the researchers can be 95% sure that the true value of the data lies.
Figure - The equations used to work out the error factor and the confidence intervals of cohort and case control studies
SimpleMed original by Maddie Swannack
The confidence interval is worked out through a number called the error factor. This is worked out according to an equation specific to the study design, as shown here.
- In the case control study, the letters a-d in the error factor equation reflect the values in the table used in this study design.
- In the cohort study equation, d1 and d2 represent the cases in population 1 (exposed) and the cases in population 2 (unexposed).
The confidence interval (CI) is worked out using the error factor, and one piece of data from the study (notated here for clarity as the randomly chosen symbol ꝋ). To find the lower bound of the CI, ꝋ is divided by the error factor. To find the upper bound of the CI, ꝋ is multiplied by the EF. The CI is the distance between the lower and upper bound.
Working out Confidence Intervals
ꝋ is a symbol randomly assigned to represent the data chosen from the study to work out the CI. Its true value is as follows:
- The CI for a case control study uses the odds ratio (OR).
- The CI for a cohort study uses the incidence rate ratio (IRR).
Like previously mentioned, confidence intervals are the range of values around the study value where the true value could lie. There is some doubt because studies cannot guarantee to be correct 100% of the time.
Confidence Intervals – Cross Sectional Study Design
The equation used for working out the confidence intervals for cross sectional study design is different to the type used for cohort and case control studies. This is because in a cross sectional study, there is only one result (the proportion) rather than in the other designs where you might have two or more. This equation can seem a little confusing at the start, but it will be gone through step by step.
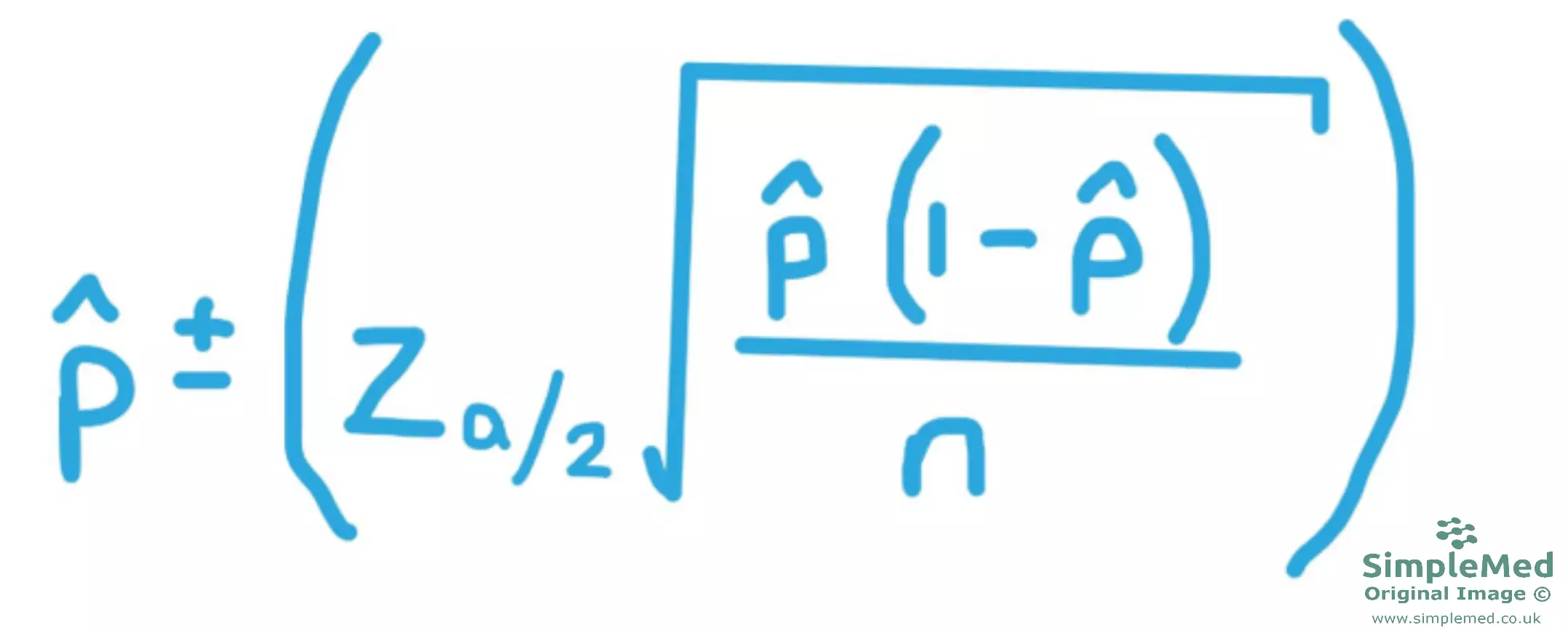
Figure - The equation used to find the confidence interval of a cross sectional study
SimpleMed original by Maddie Swannack
This is the equation used to work out the confidence intervals in cross sectional studies. An extra set of brackets (the larger ones) to help aid clarity when considering the order of operations.
In this example, the study results will be that out of 500 households observed, 337 had one or more member of that household currently under 18 (called ‘child’).
This means we need to find the proportion of households with one child in, out of the total sample size of 500 (represented by the letter n). This means we do 337 / 500, giving us a proportion of 0.674. In this equation, this represents the symbol p̂ (called ‘p hat’).
However, it is important to remember that this sample might not be representative of the whole population, so it is important to work out a confidence interval to give a more realistic representation of the whole population. To calculate a meaningful confidence interval about the whole population proportion, there are two conditions that must be met by your sample:
- The size of your sample must be no more than 5% of the size of the population it was drawn from. This might seem counterintuitive but stick with it.
- The sample must have approximately a normal distribution. This can often be met by random sampling.
This next section will be the same regardless of the study results, so long as they are using a 95% confidence interval:
Next we have to work out the 95% confidence interval. This means that there is 5% of the distribution not included in our confidence interval, called α (alpha). Using the diagram below, we can see that 95% of the distribution is in the centre, leaving 2 2.5% ‘tails’ either side of this central portion, making up the 5% of the distribution that is called α. This means that α=0.05 and α/2=0.025.Then, we use a Z table. This is a complicated table used to work out the number of standard deviations from the mean that the 5% not included in our study are. It is basically a list of numbers.
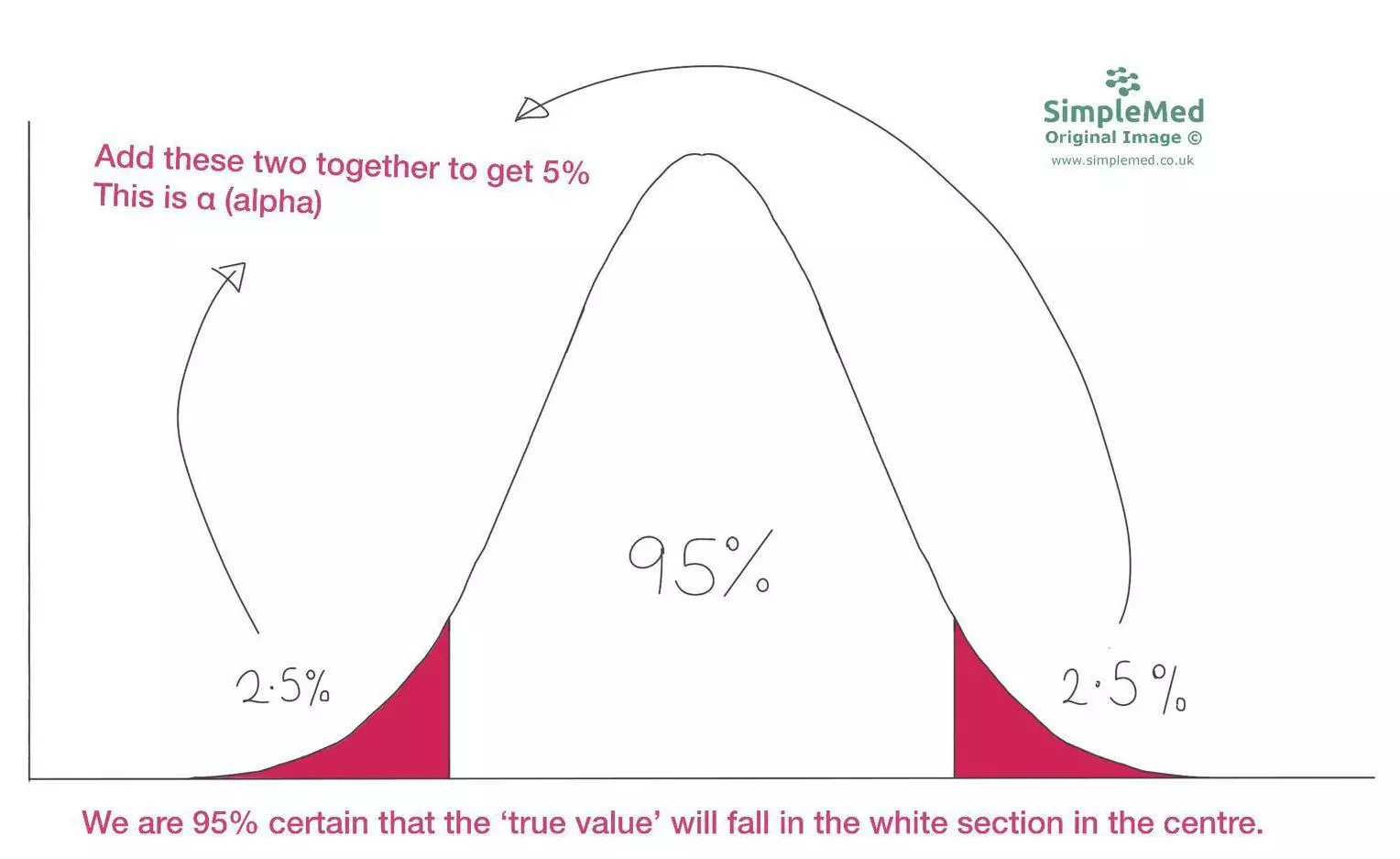
Graph: Demonstrates a normal distribution
SimpleMed Original by Maddie Swannack
Then, we use a Z table. This is a complicated table used to work out the number of standard deviations from the mean that the 5% not included in our study are. It is basically a list of numbers, and the Z score for 95% confidence intervals is always 1.96. So Zα/2 = 1.96.
Now we must we put the data into the equation:
So now we have the information to plug our data into the equation.
p̂ = 0.674 – this is the part that changes based on the proportion
Zα/2 = 1.96 – this does not change so long as a 95% confidence interval is used
n = 500 – this changes depending on the sample size
Remember that the equation must be done twice: the first time using p̂ PLUS Zα/2 to find the upper bound of the confidence interval, and the second time using p̂ MINUS Zα/2 to find the lower bound of the confidence interval.
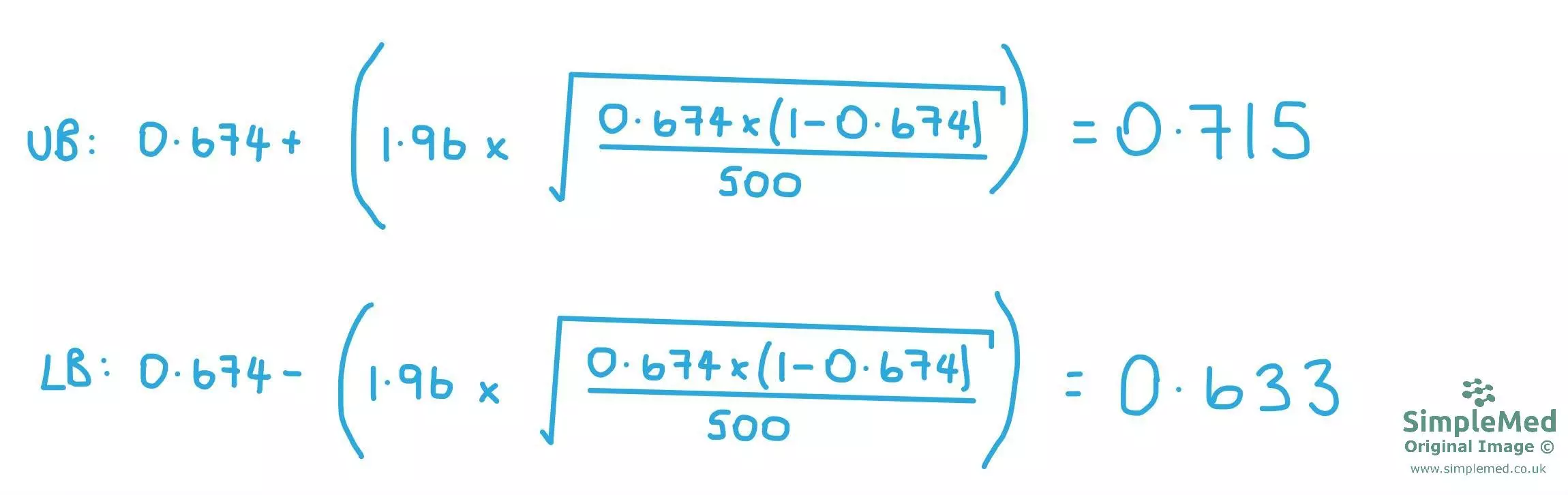
Diagram - shows the equations used to work out the upper bound (UB) and the lower bound (LB) of the confidence interval in our study.
SimpleMed original by Maddie Swannack
Working out Statistical Significance
Whether a study’s results are ‘statistically significant’ is a characteristic of the confidence interval.
If the value of the null hypothesis is within the confidence interval, the results are not significant, because the results of the study could indicate that ‘there is no difference’. This applies to all study designs that can have a confidence interval worked out (case control, cohort and cross sectional).
If a study is using a calculated ratio, the null hypothesis would be that the independent variable (the thing that is being changed in the study) has had no effect on the outcome. This is represented by the value of ‘1’, because no difference in a ratio is when the numbers are the same, aka the ratio is 1:1.
If the confidence interval includes the number 1 in this case, the true value could be 1, meaning there could be no difference. This means that the null hypothesis should be accepted, and the correct phrasing of this is: “The number 1 is included in the confidence interval, meaning that the confidence interval is large enough to include the null hypothesis. This means there could be no difference, the null hypothesis should be accepted, and the results are not statistically significant.”
If a study is not using ratio but is using the difference between two numbers (so the numbers are subtracted one from the other) then the null hypothesis should be represented by 0. This is because when subtracting numbers, the ‘no difference’ value is 0.
In this case, if the confidence interval includes the number 0, the true value could be 0, meaning there could be no difference. This means that the null hypothesis should be accepted, and the correct phrasing is: “The number 0 is included in the confidence interval, meaning that the confidence interval is large enough to include the null hypothesis. This means there could be no difference, the null hypothesis should be accepted, and the results are not statistically significant.”
A common pitfall here is saying things like “the confidence interval contains the study value”. This will always be true, because the confidence interval is a range based around that value. It should be the null hypothesis value that is important (1 if using ratios, 0 if using the difference between numbers). It is whether the null hypothesis value is within the confidence interval that is important.
Examples of Confidence Intervals
A case control study classifies patients based on their disease state (lung cancer or not lung cancer) and investigates past exposure.
The results are as follows:
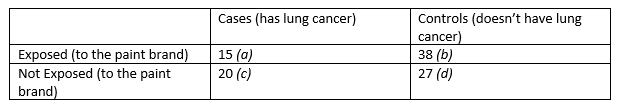
The odds ratio is worked out by doing ad / bc which in this case is (15 x 27) / (38 x 20) = 0.5328
The error factor in a case control study is worked out by doing e ^ {2 x √( 1/a + 1/b + 1/c + 1/d) } That means in this case the error factor is e ^ {2 x √( 1/15 + 1/38 + 1/20 + 1/27) } which is equal to 0.3600
The confidence interval upper bound is worked out by doing OR/EF = 1.48
The confidence interval lower bound is worked out by doing ORxEF = 0.1918
This means that the odds ratio has a 95% chance of being between 0.1918 and 1.480.
Because the odds ratio crosses the value of 1 (representing the null hypothesis that there is no assocaition between this brand of paint and lung cancer), it means the results of this study are not statistiucally significant, and the null hypothesis should be accepted.
A cohort study classifies people based on their exposure state (second hand smoke) and investigates the occurance of lung cancer.
The results are as follows:
In the exposed group: 127/295 people developed lung cancer with an average of 8 person years in the study. The incidence rate for this population is 127 / 8 = 15.875 cases per person year.
In the unexposed group: 52/229 people developed lung cancer. This group does not have any person years at risk because they are the control group. The incidence rate in this group is 52 / 8 = 6.5 cases per person year.
This means that the incidence rate ratio is 15.875 / 6.5 = 2.44. This means that there is 2.44 more chance of developing lung cancer according to this study.
The error factor in a case control study is worked out by doing e ^ {2 x √( 1/d1 + 1/d2) } That means in this case the error factor is e ^ {2 x √( 1/15 + 1/38 + 1/20 + 1/27) } which is equal to 0.3600
Upper bound of the confidence interval = 2.44 x 0.36 = 0.8784
Lower bound of the confidence interval = 2.44 / 0.36 = 6.778
We are therefore 95% confident that the true value of the study is between 0.8784 and 6.778
Because the null hypothesis is represented by the value of 1, and the confidence interval is including the value of 1, the results of this study are NOT statistically significant.
Edited by: Dr. Marcus Judge and Dr. Ben Appleby
- 7074
