Membrane Potentials

Core

What is a Membrane Potential?

A membrane potential is the magnitude of an electrical charge across a plasma membrane, expressed as the potential inside the cell relative to the extracellular solution. It is measured in millivolts (mV).

All cells have a membrane potential, although the resting membrane potential and ability to change the membrane potential (excitability) varies between different cell types. Membrane potentials provide the basis of cell signalling in all cells.

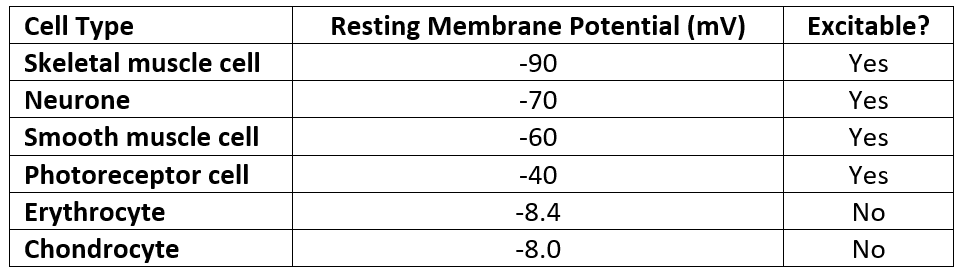
Table - The resting membrane potentials of different cell types

SimpleMed original by Dr. Joshua Bray

The establishment of a membrane potential requires two key criteria:

1. Ionic concentration gradients (resulting in an asymmetrical distribution of ions)
2. Selective permeability to particular ions (via channels) - Mainly K⁺, Na⁺ and Cl^-

The movement of ions results in a separation of charge across the membrane: this is the membrane potential.

The Na⁺/K⁺ pump is slightly electrogenic, contributing a small negative component to the resting membrane potential. However, it is indirectly responsible for the entire membrane potential as it sets up and maintains the ionic gradients required to generate the membrane potential.

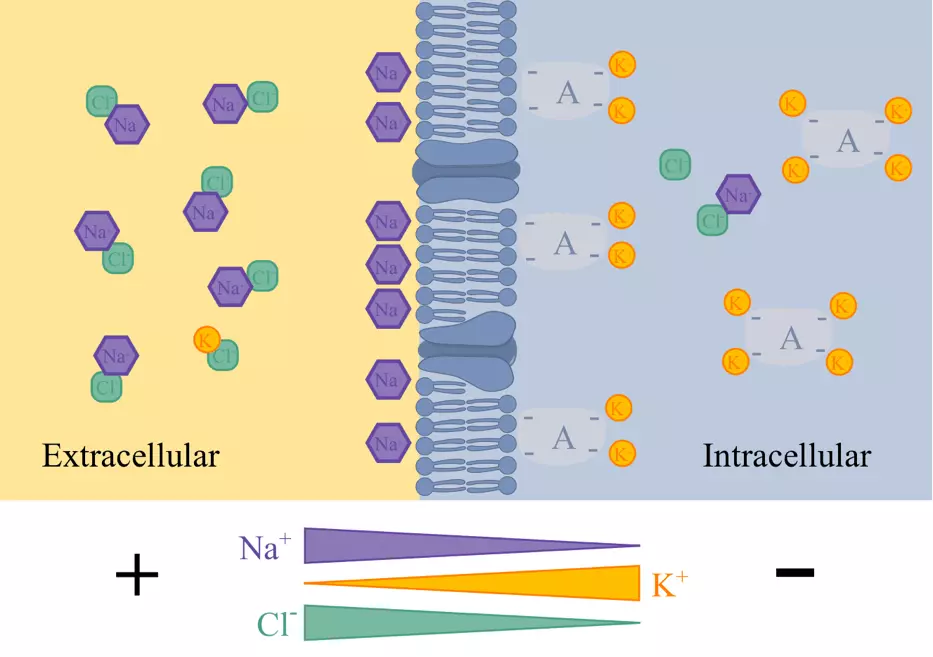
Diagram - The ionic concentration gradients responsible for the membrane potential

Creative commons source by smonsays [CC BY-SA 4.0 (https://creativecommons.org/licenses/by-sa/4.0)]

The Resting Membrane Potential

There are two gradients which determine the net movement of ions:

1. Chemical gradient - Equivalent to the concentration gradient.
2. Electrical gradient - The tendency of positive ions to move to areas of negative charge and negative ions to move to areas of positive charge.

Assume that the membrane is selectively permeable to one ion only - for example, K⁺. If the concentration of K⁺ is greater inside the cell compared to outside the cell, then K⁺ will begin to move out of the cell. However, as K⁺ leaves the cell, the cell will become less positive and the extracellular solution will become more positive - this causes the opposing electrical gradient to increase. When the chemical and electrical gradients become equal and opposite, they cancel each other out so that there is no net movement of K⁺. However, a negative charge remains across the membrane: the resting membrane potential.

The membrane potential when the membrane is selectively permeable to only one type of ion is known as the equilibrium potential (E) for that ion. We can calculate an ion’s equilibrium potential using the Nernst equation. The Nernst equation for K⁺ is as follows: E_K = (RT/zF) ln([K⁺]_out/[K⁺]_in), where R is the gas constant (8.314 J mol^-1 K^-1), T is temperature (K), z is the charge on the ion, F is the Faraday constant (96500 C mol^-1) and [K⁺]_in/out are the concentrations of K⁺ inside and outside the cell respectively.

To make calculations easier, we can work out the value of RT/F (T = 37^oC) and convert the natural log (ln) to log10. This gives us: E_K = 61/z. log10( [K⁺]_out/[K⁺]_in).

The Nernst equation can be used for any ion (both positive and negative ions).

If a membrane is selectively permeable to K⁺ alone, its membrane potential will be at E_K. However, in reality this never actually happens, as real cells are permeable to other ions too.

The equilibrium potentials of K⁺, Na⁺ and Cl^- at physiological temperature and concentrations are as follows:

• E_K = -95 mV
• E_Na = +60 mV
• E_Cl = -70 mV to -90 mV

Changing the Membrane Potential

The membrane potential can be changed by altering the membrane’s permeability to different ions - i.e. opening and closing ion channels.

If the membrane becomes more permeable to an ion, it will cause the membrane potential to shift towards the equilibrium potential for that ion.

The value of the membrane potential can change in two directions:

• Depolarisation - The membrane potential becomes less negative
• Hyperpolarisation - The membrane potential becomes more negative

Opening Na⁺ or Ca²⁺ channels usually results in depolarisation, whereas opening K⁺ or Cl^- channels usually results in hyperpolarisation. The actual effect depends on the ion equilibrium potential relative to the current membrane potential.

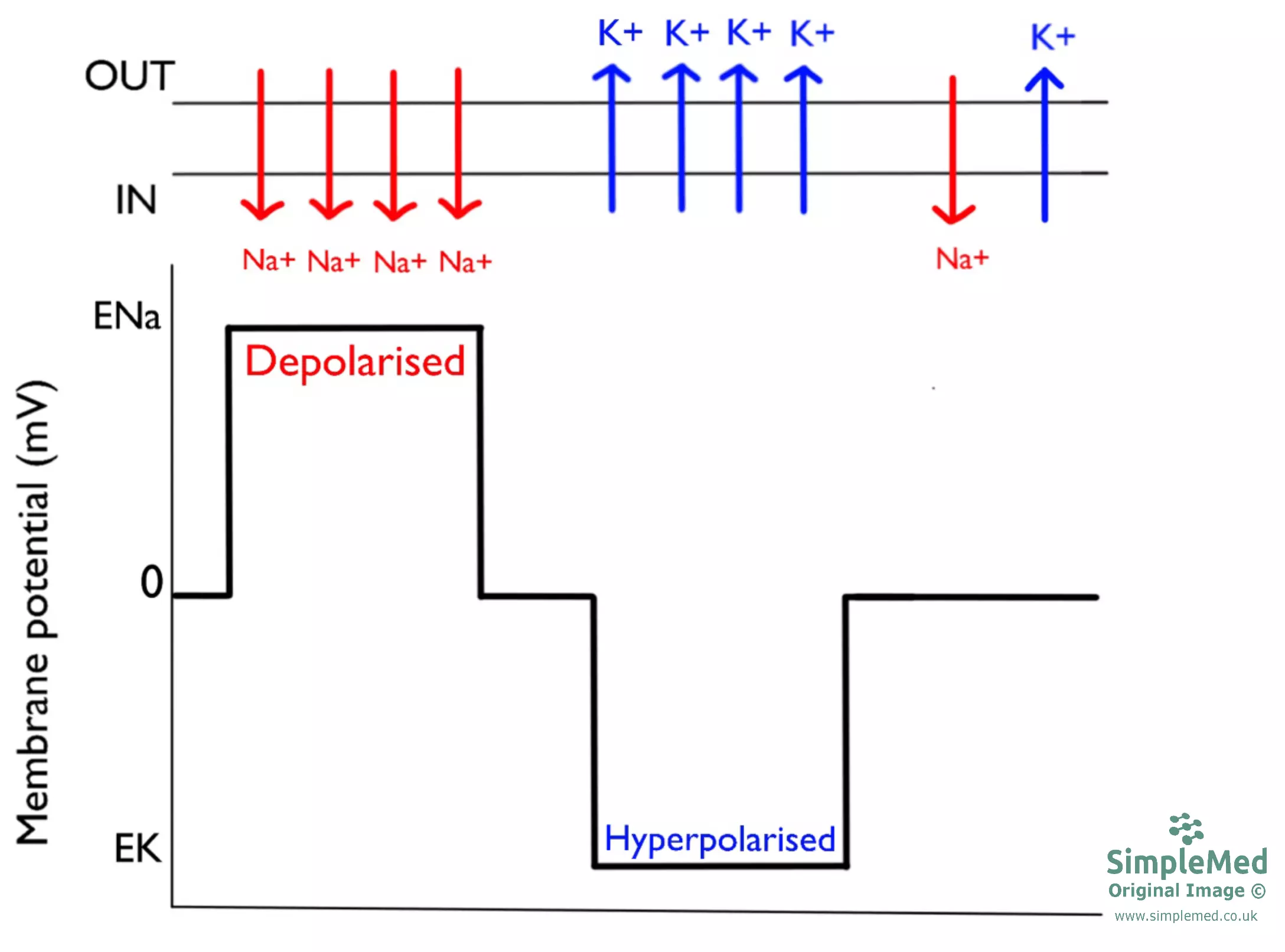
Diagram - Graph showing the changes in membrane potential by altering Na⁺ and K⁺ flow

SimpleMed original by Dr. Joshua Bray

Synaptic Transmission

A synapse is a connection between two excitable cells, where a chemical neurotransmitter is released from the pre-synaptic cell, diffuses across the synaptic cleft and binds to receptors on the post-synaptic membrane. This allows the conversion of an electrical signal (action potential) to a chemical signal (neurotransmitter), which generates a new electrical signal in the post-synaptic cell.

Synaptic transmission can be classed as fast or slow:

• Fast transmission - Involves ligand-gated ion channels (e.g. nicotinic acetylcholine receptors), which open in response to neurotransmitter binding.
• Slow transmission - Involves G-protein coupled receptors (e.g. muscarinic acetylcholine receptors), which activate channels via direct and indirect signalling pathways.

Synapses can also be excitatory or inhibitory:

• Excitatory synapses cause membrane depolarisation - Transmitters commonly include glutamate and, depending on receptor type, dopamine and acetylcholine
• Inhibitory synapses cause membrane hyperpolarisation - Transmitters commonly include GABA and glycine

The more depolarised the post-synaptic cell becomes, the more likely it is to reach the threshold for action potential generation.

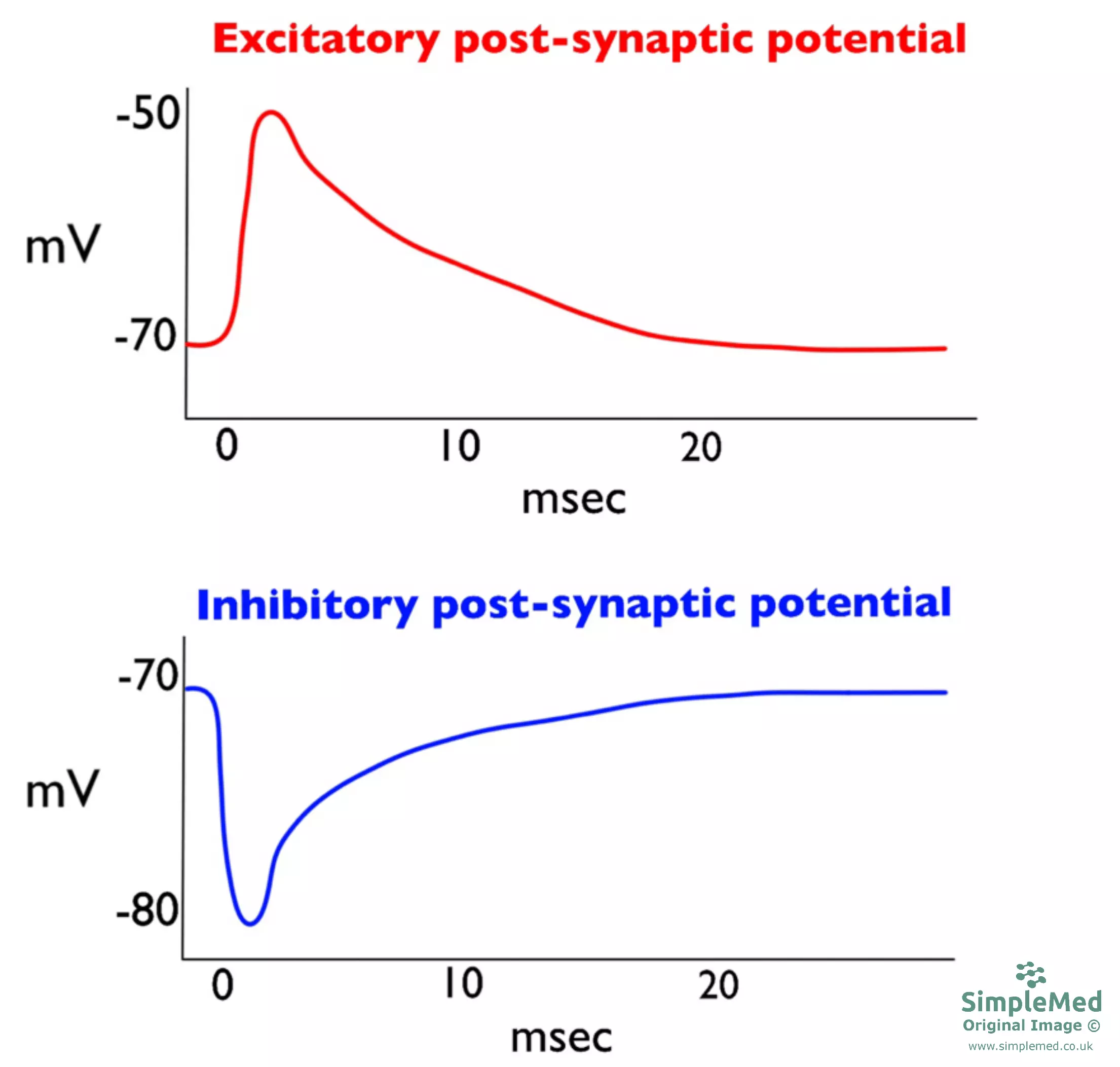
Diagram - Graphs showing the excitatory and inhibitory post-synaptic potentials

SimpleMed original by Dr. Joshua Bray

Reviewed by: Dr. Thomas Burnell

Quiz

Preview the Membrane Potentials quiz